Next: Der Crab-Pulsar und Supernovaüberrest Up: No Title Previous: Welche Vorkenntnisse sollten Sie
![]()
![]()
![]()
Next: Der Crab-Pulsar und Supernovaüberrest
Up: No Title
Previous: Welche Vorkenntnisse sollten Sie
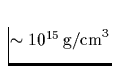 die Dichte von Kernmaterie und die Schwerebeschleunigung
an der Sternoberfläche ist mehr als zehnbillionenmal größer als auf der Erde.
Mit ihren riesigen Magnetfeldstärken von bis zu
die Dichte von Kernmaterie und die Schwerebeschleunigung
an der Sternoberfläche ist mehr als zehnbillionenmal größer als auf der Erde.
Mit ihren riesigen Magnetfeldstärken von bis zu 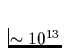 Gauß, und
Rotationsperioden im Millisekundenbereich, verkörpern die als Pulsare beobachtbaren
Neutronensterne Extremzustände in nahezu allen stellaren Parametern und stellen
damit ein physikalisches Laboratorium zu Verfügung, wie es auf der Erde nie erreicht
werden kann.
Gauß, und
Rotationsperioden im Millisekundenbereich, verkörpern die als Pulsare beobachtbaren
Neutronensterne Extremzustände in nahezu allen stellaren Parametern und stellen
damit ein physikalisches Laboratorium zu Verfügung, wie es auf der Erde nie erreicht
werden kann.
Wann entsteht ein Neutronenstern ?
Das endgültige Schicksal eines Sterns wird im wesentlichen durch seine
Anfangsmasse bestimmt. Wenn auch die exakten Massengrenzen bisher nicht
sehr genau bekannt sind, so gilt doch in etwa das folgende: Liegt
die anfängliche Masse eines Sterns im Bereich von 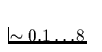 Sonnenmassen
Sonnenmassen 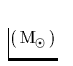 , so gibt der Stern Masse ab bis er
sich zu einem Weißen Zwerg entwickelt hat oder explodiert als Typ-Ia
Supernova in einer nuklearen C-Detonation, sofern sich der Stern
in einem Binärsystem befindet. Ist die anfängliche Masse größer
als ungefähr 8-10
, so gibt der Stern Masse ab bis er
sich zu einem Weißen Zwerg entwickelt hat oder explodiert als Typ-Ia
Supernova in einer nuklearen C-Detonation, sofern sich der Stern
in einem Binärsystem befindet. Ist die anfängliche Masse größer
als ungefähr 8-10 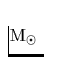 , so erwartet man die Entstehung
eines Neutronensterns in Verbindung mit einer als Typ Ib, Ic oder II
klassifizierten Supernovaexplosion (Hillebrandt 1997). Für Sternmassen
oberhalb von etwa 30
, so erwartet man die Entstehung
eines Neutronensterns in Verbindung mit einer als Typ Ib, Ic oder II
klassifizierten Supernovaexplosion (Hillebrandt 1997). Für Sternmassen
oberhalb von etwa 30 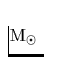 wird die Entstehung eines Neutronensterns
dagegen unwahrscheinlich, der Stern kollabiert der Theorie nach zu
einem Schwarzen Loch.
wird die Entstehung eines Neutronensterns
dagegen unwahrscheinlich, der Stern kollabiert der Theorie nach zu
einem Schwarzen Loch.
Warum beobachtet man Neutronensterne im Röntgenbereich ?
Aufgrund der gewaltigen Verdichtung der Materie während des Sternkollaps
erreicht die Temperatur innerhalb eines Neutronensterns in statu nascendi
einen Wert von einigen hundert Milliarden Grad und kühlt danach durch die
Abstrahlung von Neutrinos aus dem Neutronensternkernbereich innerhalb nur
weniger Stunden bis Tage auf etwa eine Milliarde Grad ab. Folgt man im
weiteren Verlauf der thermischen Evolution den Voraussagen der
Neutronensternkühlungsmodelle, so sollte - abhängig von den
Eigenschaften der Materie bei nuklearer Dichte - die Oberflächentemperatur
von Neutronensternen für mindestens einhunderttausend Jahre mehr als etwa
eine Million Grad betragen, so daß das Emissionsmaximum ihrer thermischen
Strahlung im weichen Röntgenbereich liegt und bei nicht zu starker
interstellarer Absorption mit dem Röntgensatelliten ROSAT beobachtet
werden kann.
Warum studiert man die thermische Evolution von Neutronensterne ?
Ein möglicher Zugang zur experimentellen Untersuchung der Materie bei
extremer Energie- und Baryonendichte ergibt sich aus der engen
Verbindung zwischen der thermischen Evolution von Neutronensternen und
den physikalischen Eigenschaften der Neutronensternmaterie bei nuklearer
Materiedichte. Je nach Neutronensternmodell und den darin enthaltenen
Annahmen bezüglich der internuklearen
hadronischen Wechselwirkung, der Existenz von Pionen, Kaonen, Hyperonen
oder Quarks im Kern des Neutronensterns sowie den Einflüssen der superfluiden
Neutronen in der inneren Neutronensternkruste (näheres hierzu
in Anhang A), liefern die Theorien verschiedene Kühlraten und
damit unterschiedliche Voraussagen für die Oberflächentemperatur eines
Neutronensterns als Funktion seines Alters. Vergleicht man die für eine
spezielle Modell-Zustandsgleichung berechnete Neutronensternkühlkurve mit
den von ROSAT gemessenen Neutronensterntemperaturen, so erlaubt dies wichtige
Rückschlüsse für die Richtigkeit der zur Bildung der Zustandsgleichung
gemachten Annahmen und liefert die notwendigen experimentellen Grundlagen
zur Verifikation der theoretischen Modelle.
Röntgenstrahlung thermischen Ursprungs stellt für die hier besprochene
Klasse der sogenannten rotationsgetriebenen Pulsare (von denen der Crab-Pulsar
der jüngste Vertreter ist) nur eine von mehreren möglichen Emissionsmechanismen
dar. Eine weiterer, sehr wichtige Strahlungskomponente, ist die der nicht-thermischen
Strahlung, wie sie beispielsweise von geladenen Teilchen emittiert wird die sich
entlang von (gekrümmten) Magnetfeldlinien bewegen. Wie im nächsten Kapitel noch
näher besprochen wird, ist die nicht-thermische Strahlung beim Crab-Pulsar
sogar die mit Abstand dominierende Strahlungskomponente.
Was ist ein rotationsgetriebener Pulsar ?
Insgesamt kennt man bis heute etwa 750 Neutronensterne die als rotationsgetriebene
Pulsare in Erscheinung treten. Ihre charakteristische Pulsarstrahlung ist eine
unmittelbare Folge des extremen Neutronensternmagnetfeldes, das in Verbindung mit der
schnellen Rotation des Sterns gleichsam wie ein gigantischer Dynamo wirkt und geladene
Teilchen in einem engen Strahlenbündel oberhalb der Magnetfeldpole auf nahezu
Lichtgeschwindigkeit beschleunigt (vergl. dazu die Abb. 1). Die
beschleunigten Teilchen emittieren bei ihrer spiralförmigen Bewegung entlang
der gekrümmten Magnetfeldlinien eine intensive, breitbandige elektromagnetische
Strahlung, die sogenannte Synchrotron- und Krümmungsstrahlung. Fällt in einem
solchen Szenario die Magnetfeldachse des Neutronensterns nicht mit seiner
Rotationsachse zusammen, so kreist das Strahlenbündel - ähnlich dem Leuchtfeuer
eines Leuchtturms - um die Rotationsachse des Neutronensterns, und ein Beobachter
innerhalb des Strahlungskegel registriert für einen kurzen Augenblick das
Überstreichen des Strahlenbündels als Puls in seinen Meßinstrumenten.
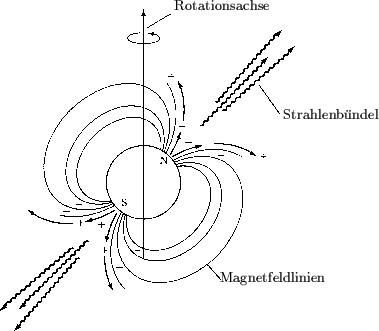
Im Gegensatz zu den sogenannten akkretierenden Neutronensternen, bei denen
Materie von einem nahen Begleitstern oder aus dem interstellaren Medium
auf den Neutronenstern übergeht (kosmischer Staubsauger) und dabei
intensive Röntgenstrahlung aussendet, spricht man von einem
rotationsgetriebenen Pulsar, wenn die Summe der pro Zeiteinheit vom
Pulsar (bzw. dem mit ihm mit-rotierenden Magnetfeld) abgestrahlten
Energie gerade der Abnahme seiner Rotationsenergie entspricht. Diese
Bedingung (Energiebilanz) ist bisher nur beim Crab-Pulsar nachprüfbar
und dort in sehr guter Näherung erfüllt.
Bezeichnet ![]() das Trägheitsmoment des Neutronensterns (der
kanonischer Wert ist hier
das Trägheitsmoment des Neutronensterns (der
kanonischer Wert ist hier 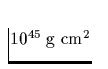 - warum?,
nehmen Sie an M=1.4
- warum?,
nehmen Sie an M=1.4 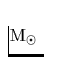 , R=10 km) und
, R=10 km) und ![]() seine Winkelgeschwindigkeit
(zum Beispiel die des Crab-Pulsars, der eine Rotationsperiode von P=33.4
Millisekunden besitzt und demnach mit einer Winkelgeschwindigkeit von
seine Winkelgeschwindigkeit
(zum Beispiel die des Crab-Pulsars, der eine Rotationsperiode von P=33.4
Millisekunden besitzt und demnach mit einer Winkelgeschwindigkeit von
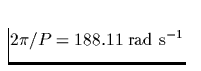 rotiert), so beträgt die im Neutronenstern
gespeicherte Rotationsenergie
rotiert), so beträgt die im Neutronenstern
gespeicherte Rotationsenergie![]()
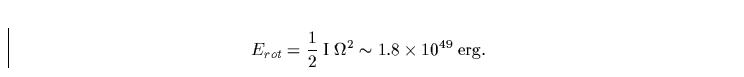
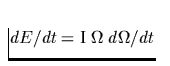 , was sich experimentell durch die Zunahme der
Neutronensternrotationsperiode bemerkbar macht. Beim Crab-Pulsar beträgt
die Abnahme der Rotationsenergie beispielsweise
, was sich experimentell durch die Zunahme der
Neutronensternrotationsperiode bemerkbar macht. Beim Crab-Pulsar beträgt
die Abnahme der Rotationsenergie beispielsweise 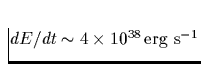 und die Zunahme der Rotationsperiode
und die Zunahme der Rotationsperiode
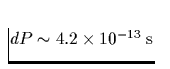 pro Sekunde.
pro Sekunde.
Es ist eine schöne Übung zur Praktikumsvorbereitung (die nur Grundlagen
der Elektrodynamik voraussetzt) aus der zeitlichen Änderung der
Neutronensternrotationsenergie 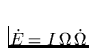 sowie
aus der pro Zeiteinheit abgestrahlten Energie des rotierenden magnetischen
Dipols
sowie
aus der pro Zeiteinheit abgestrahlten Energie des rotierenden magnetischen
Dipols 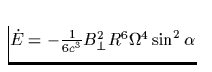 den
funktionellen Zusammenhang zwischen Magnetfeldstärke und den Observablen
den
funktionellen Zusammenhang zwischen Magnetfeldstärke und den Observablen
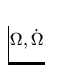 (bzw.
(bzw. 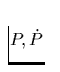 ) sowie zwischen dem Bremsalter
) sowie zwischen dem Bremsalter
![]() (auch als spin-down age bezeichnet) und
(auch als spin-down age bezeichnet) und 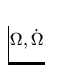 (bzw.
(bzw. 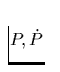 ) abzuleiten.
) abzuleiten.
Nützliche Formeln hierzu sind: 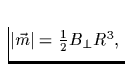
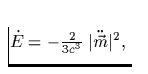 sowie
sowie 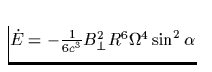 . Dabei bedeuten
. Dabei bedeuten ![]() das
magnetische Moment des rotierenden Dipols,
das
magnetische Moment des rotierenden Dipols, 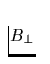 die Senkrechtkomponente
das magnetischen Dipolfeldes an den Polen, c die
Lichtgeschwindigkeit,
die Senkrechtkomponente
das magnetischen Dipolfeldes an den Polen, c die
Lichtgeschwindigkeit, 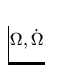 die Winkelgeschwindigkeit sowie
deren zeitliche Ableitung und
die Winkelgeschwindigkeit sowie
deren zeitliche Ableitung und ![]() den Winkel zwischen Rotationsachse
und Magnetfeldachse (nehmen sie der Einfachheit halber
den Winkel zwischen Rotationsachse
und Magnetfeldachse (nehmen sie der Einfachheit halber 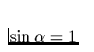 an -
aligned rotator). R bezeichnet den Neutronensternradius (z.B. R=10
km). Zur Ableitung des Bremsalters müssen Sie ferner annehmen
an -
aligned rotator). R bezeichnet den Neutronensternradius (z.B. R=10
km). Zur Ableitung des Bremsalters müssen Sie ferner annehmen 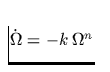 wobei k=const und
wobei k=const und 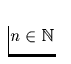 . Ferner nimmt man an, daß
die (heute) gemessene Winkelgeschwindigkeit des Pulsars sehr klein ist gegenüber
der Winkelgeschwindigkeit
. Ferner nimmt man an, daß
die (heute) gemessene Winkelgeschwindigkeit des Pulsars sehr klein ist gegenüber
der Winkelgeschwindigkeit ![]() kurz nach der Entstehung des Neutronensterns
(man kann in diesem Fall gewissen Terme in der Ableitung vernachlässigen). n
bezeichnet man als Bremsindex.
kurz nach der Entstehung des Neutronensterns
(man kann in diesem Fall gewissen Terme in der Ableitung vernachlässigen). n
bezeichnet man als Bremsindex.
Rotationsgetriebene Pulsare wie der Crab-Pulsar werden hauptsächlich als Radiopulsare beobachtet. Ihre Röntgen- und Gamma-Strahlung wird in der Erdatmosphäre absorbiert und ist mit den heute zur Verfügung stehenden Satelliten aufgrund ihrer beschränkten Empfindlichkeit nur dann nachweisbar, wenn der Neutronenstern entweder sehr jung oder sehr nah ist. Bis heute sind nur 27 der insgesamt 750 rotationsgetriebenen Pulsare auch im Röntgenbereich nachgewiesen, und sogar nur sieben davon auch im Gamma-Bereich oberhalb von 100 GeV. Im optischen Wellenlängenbereich hat man bisher nur Strahlung von acht rotationsgetriebenen Pulsare detektiert. Der Crab-Pulsar ist der einzige Neutronenstern dessen Strahlung über das gesamte elektromagnetische Spektrum nachgewiesen ist.
Roberto Saglia