Next: Der zentrale Kernbereich des Up: Der innere Aufbau von Previous: Die äußere Neutronensternkruste
![]()
![]()
![]()
Next: Der zentrale Kernbereich des
Up: Der innere Aufbau von
Previous: Die äußere Neutronensternkruste
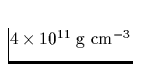 ist das
letzte Neutron in 118Kr nur noch schwach an den Kern gebunden, so daß
die Neutronen vom Kern abzuwandern beginnen und eine entartete Flüssigkeit
bilden, sobald die Dichte einen Wert von
ist das
letzte Neutron in 118Kr nur noch schwach an den Kern gebunden, so daß
die Neutronen vom Kern abzuwandern beginnen und eine entartete Flüssigkeit
bilden, sobald die Dichte einen Wert von 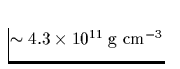 (neutron drip point) überstiegen hat (Baym et al 1971). Bei weiter
ansteigendem Druck werden dann die zu Kristallgittern organisierten Kerne
(Schmelztemperatur
(neutron drip point) überstiegen hat (Baym et al 1971). Bei weiter
ansteigendem Druck werden dann die zu Kristallgittern organisierten Kerne
(Schmelztemperatur 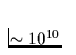
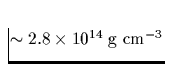 berühren
und ineinander eintauchen. Es bildet sich eine Flüssigkeit aus
nicht-relativistischen entarteten Neutronen und Protonen sowie
relativistischen Elektronen, wobei für die Neutronen unterhalb
von
berühren
und ineinander eintauchen. Es bildet sich eine Flüssigkeit aus
nicht-relativistischen entarteten Neutronen und Protonen sowie
relativistischen Elektronen, wobei für die Neutronen unterhalb
von 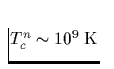 der Phasenübergang in den
superfluiden Zustand möglich ist (Ginzburg 1969, Weisskopf
1981, Alpar & Pines 1993). Jeweils zwei Neutronen mit entgegensetztem Spin
und Impuls bilden dabei ein sogenanntes Cooper-Paar, dessen Gesamtspin sich
zu Null addiert und das sich deshalb in vieler Hinsicht wie ein Boson
verhält.
Obwohl die Auswirkung der Superfluidität auf die Zustandsgleichung der
inneren Kruste nur von vernachlässigbarer Größenordnung ist
(die Paarungsenergie der Cooper-Paare beträgt weniger als 1% der
gesamten hadronischen Wechselwirkungsenergie in dieser Region), so sind
doch die Konsequenzen für die physikalischen Eigenschaften des
Neutronensterns von ganz entscheidender Bedeutung. Sie reichen von der
Beeinflussung der Magnetfeldevolution bei Millisekundenpulsaren und der
tektonischen Plattenbewegung der Neutronensternkruste (Ruderman 1993)
bis zur Bestimmung des Glitch
der Phasenübergang in den
superfluiden Zustand möglich ist (Ginzburg 1969, Weisskopf
1981, Alpar & Pines 1993). Jeweils zwei Neutronen mit entgegensetztem Spin
und Impuls bilden dabei ein sogenanntes Cooper-Paar, dessen Gesamtspin sich
zu Null addiert und das sich deshalb in vieler Hinsicht wie ein Boson
verhält.
Obwohl die Auswirkung der Superfluidität auf die Zustandsgleichung der
inneren Kruste nur von vernachlässigbarer Größenordnung ist
(die Paarungsenergie der Cooper-Paare beträgt weniger als 1% der
gesamten hadronischen Wechselwirkungsenergie in dieser Region), so sind
doch die Konsequenzen für die physikalischen Eigenschaften des
Neutronensterns von ganz entscheidender Bedeutung. Sie reichen von der
Beeinflussung der Magnetfeldevolution bei Millisekundenpulsaren und der
tektonischen Plattenbewegung der Neutronensternkruste (Ruderman 1993)
bis zur Bestimmung des Glitch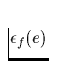 besitzen würde.
besitzen würde.
Roberto Saglia