Next: Bestimmung einer oberen Schranke Up: Die Photonen-Ankunftszeitanalyse Previous: Die Baryzentrums-Korrektur: UTC TDB
![]()
![]()
![]()
Next: Bestimmung einer oberen Schranke
Up: Die Photonen-Ankunftszeitanalyse
Previous: Die Baryzentrums-Korrektur: UTC TDB
![\begin{displaymath}
\phi_i(t_{ref}) = \mbox{Bruchteil von}\;\left[ f\cdot (t_i-t...
...f}) + \frac{1}{2}\cdot
\dot{f}\cdot (t_i-t_{ref})^2 \right]\,.\end{displaymath}](img169.gif) |
(4) |
Darin entsprechen f=f(tref) der zum Zeitpunkt der Referenz-Epoche
tref gültigen Rotationsfrequenz sowie 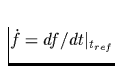 den zugehörigen Werten der ersten zeitlichen Ableitung der Frequenz
zum Zeitpunkt tref. ti mit
den zugehörigen Werten der ersten zeitlichen Ableitung der Frequenz
zum Zeitpunkt tref. ti mit 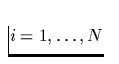 kennzeichnet die korrigierten
Photonenankunftszeiten der insgesamt N Röntgenphotonen und
kennzeichnet die korrigierten
Photonenankunftszeiten der insgesamt N Röntgenphotonen und
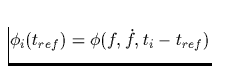 den nicht ganzzahligen
Anteil der zum Zeitpunkt (ti-tref) gehörenden Pulsarphase ('residual
phase').
Eine exakte Kenntnis der benutzten Pulsarephemeriden
den nicht ganzzahligen
Anteil der zum Zeitpunkt (ti-tref) gehörenden Pulsarphase ('residual
phase').
Eine exakte Kenntnis der benutzten Pulsarephemeriden 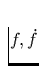 und tref stellt dabei eine der wesentlichen Voraussetzungen für die
Anwendbarkeit dieses Verfahrens dar. Für die Bildung einer Pulsarlichtkurve
unterteilt man den eine Rotation überdeckenden Phasenbereich von
und tref stellt dabei eine der wesentlichen Voraussetzungen für die
Anwendbarkeit dieses Verfahrens dar. Für die Bildung einer Pulsarlichtkurve
unterteilt man den eine Rotation überdeckenden Phasenbereich von
![$[\,0,1\,]\cdot 2\pi$](img174.gif) in diskrete Phasenabschnitte und sortiert dem Wert von
in diskrete Phasenabschnitte und sortiert dem Wert von
![]() entsprechend die N Röntgenphotonen in die jeweiligen
Phasenabschnitte.
entsprechend die N Röntgenphotonen in die jeweiligen
Phasenabschnitte.
Roberto Saglia