Bestimmung einer oberen Schranke für den Röntgenfluß einer nicht detektierten Quelle aus dem Signal-Rausch-Verhältnis 
Bestimmung einer oberen Schranke für den Röntgenfluß aus dem Signal-Rausch-Verhältnis

Ausgehend vom Signal-Rausch-Verhältnis:         $\parbox{3.5cm}{\begin{displaymath} \frac{S}{N}=\frac{N_s}{\delta N_b}= \frac{N_s}{\sqrt{N_b}}\end{displaymath}}$ $\parbox{1.5cm}{ \begin{equation}\end{equation}}$

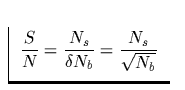
dessen Wert man formal als Standardabweichung ansehen kann, um den die für eine Quellposition ermittelte Zählrate N_s den Hintergrundbeitrag N_b übertrifft, läßt sich eine Formel zur Berechnung einer oberen Schranke für die Anzahl von Röntgenphotonen einer zu untersuchenden Himmelsregion ableiten, sofern der für diese Region festgestellte Photonenfluß unterhalb der für eine Detektion erforderlichen statistischen Nachweisgrenze liegt. Bedeutet Q die Anzahl der einer Quelle zugeordneten Photonen und 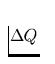$\Delta Q$ die Unsicherheit der gemessenen Größe, dann gilt zunächst:

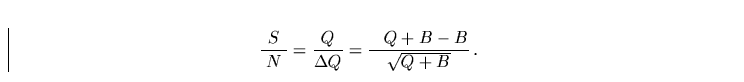$$\frac{\;S\;}{\;N\;}=\frac{\;Q\;}{\Delta Q}= \frac{\;\;\;Q + B - B}{\sqrt{Q + B}}\,.$$ (5)

Dabei bezeichnen Q die Anzahl der Quellphotonen und B die Anzahl der Hintergrundphotonen, jeweils an der Position der zu untersuchenden Quelle. Die Größe B ist dabei prinzipiell unbestimmt bzw. nur annähernd bekannt, da sich die Quelle vor dem interessierenden Hintergrund nicht entfernen läßt bzw. sich der Hintergrundbeitrag lediglich durch Interpolation eines Datensatzes ergibt, aus dem alle Quellbeiträge soweit möglich entfernt wurden.

Aus der obigen Gleichung folgt nun weiter         $\parbox{4.5cm}{\begin{displaymath} Q = S/N \times \sqrt{\;\;Q+B\;\;}\,,\end{displaymath}}$ $\parbox{1.5cm}{\begin{equation}\end{equation}}$

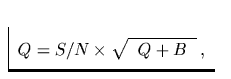
und daraus die Gleichung:             $\parbox{6.5cm}{\begin{displaymath} Q^2 - Q\cdot \left(\frac{S}{N}\right)^2 - B\cdot\left( \frac{S}{N}\right)^2 =0\,.\;\;\;\end{displaymath}}$ $\parbox{1.5cm}{\begin{equation}\end{equation}}$

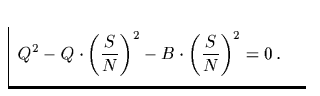
Deren Lösung lautet: $\parbox{12.1cm}{ \begin{equation} Q = \fr... ...4\;}\;\left(\frac{\;S\;}{\;N\;}\right)^2 + B\;\;}\,,\mbox{\quad}\end{equation}}$

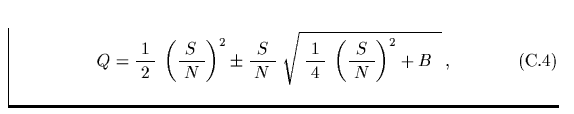
so daß sich eine obere Schranke mit einer statistischen Signifikanz von 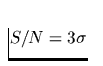$S/N = 3\sigma$ gemäß der folgenden Gleichung berechnen läßt:

 

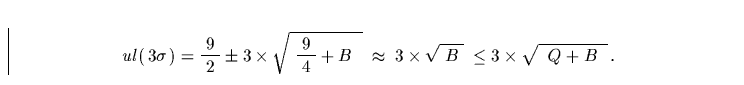$$ul(\,3\sigma\,) = \frac{\;9\;}{\;2\;} \pm 3\times \sqrt{\;\f... ...prox\; 3\times \sqrt{\;B\;}\; \le 3\times \sqrt{\;\;Q+B\;\;}\,.$$ (6)

Das heißt also, daß sich im Fall einer nicht detektierten Quelle eine obere Schranke für die Quellphotonen aus der Anzahl jener Zählerereignisse (Q+B) ergibt, die innerhalb eines auf die Quellposition zentrierten Kreisringes mit Radius 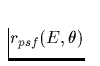$r_{psf}(E,\theta)$ registriert wurden.