Next: Über dieses Dokument ... Up: Analysetechniken Previous: Bestimmung einer oberen Schranke
![]()
![]()
![]()
Next: Über dieses Dokument ...
Up: Analysetechniken
Previous: Bestimmung einer oberen Schranke
Reicht der im Verlaufe einer Beobachtung von einer Quellposition
registrierte Photonenfluß für eine detaillierte Spektralanalyse
nicht aus, oder besitzt das verwendete Nachweisinstrument nur eine
unzureichende Energieauflösung, wie zum Beispiel der HRI-Detektor,
so lassen sich gleichwohl Informationen über die spektralen Parameter
aus dem registrierten Röntgenfluß gewinnen, wenn für das
beobachtete Objekt bereits verläßliche Schätzungen für
Sternmasse, Radius, Entfernung und Säulendichte existieren und
man - zum Beispiel gestützt auf theoretische Überlegungen -
ein Schwarzkörperspektrum für die Emission der registrierten
Strahlung zugrunde legen kann. Diese Voraussetzungen sind bei der
Untersuchung von rotationsgetriebenen Neutronensternen im allgemeinen
gut erfüllt. So folgt zum Beispiel die Distanz eines Radiopulsars
bis auf etwa 25% genau aus dem durch Radiobeobachtungen bereits
bekannten Dispersionsmaß![]() DM (Taylor & Cordes 1993). Fixiert man
darüberhinaus das Verhältnis von freien Elektronen zu
Wasserstoffatomen im interstellaren Medium, so folgt aus
DM zusätzlich eine Abschätzung für die Säulendichte NH
entlang der Sichtlinie zur Quelle, so daß man unter
Berücksichtigung der aus den Neutronensternmodellen folgenden
Abschätzungen für Masse und Radius eine obere Schranke für
die thermische Emission der untersuchten Radiopulsare und damit
eine obere Schranke für die Oberflächentemperatur dieser Objekte
berechnen kann.
DM (Taylor & Cordes 1993). Fixiert man
darüberhinaus das Verhältnis von freien Elektronen zu
Wasserstoffatomen im interstellaren Medium, so folgt aus
DM zusätzlich eine Abschätzung für die Säulendichte NH
entlang der Sichtlinie zur Quelle, so daß man unter
Berücksichtigung der aus den Neutronensternmodellen folgenden
Abschätzungen für Masse und Radius eine obere Schranke für
die thermische Emission der untersuchten Radiopulsare und damit
eine obere Schranke für die Oberflächentemperatur dieser Objekte
berechnen kann.
Die Ableitung der zur Durchführung dieser Berechnungen notwendigen
Zusammenhänge wie Simulation der interstellaren Absorptionsprozesse
und Faltung des betrachteten Spektrums mit der Detektorresponse ist
Gegenstand dieses Kapitels und basiert im wesentlichen auf der
Berechnung der für einen kühlenden Neutronenstern im
ROSAT-Energieband erwarteten Photonenzählrate.
Die zu lösende Aufgabe entspricht der Untersuchung des
Strahlungstransportes zwischen zwei vorgegeben Flächen, wobei
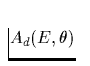 der energie- und feldwinkelabhängigen effektiven
Fläche des ROSAT-Detektors entspricht und die zweite Fläche die
Oberfläche des Neutronensterns repräsentiert.
Der Raum zwischen diesen beiden Objekten ist - entsprechend dem
interstellaren Medium - mit einem die Strahlung absorbierenden Gas
ausgefüllt, welches die vom Ort s abhängige Dichte nH(s)
besitzt und unter Beachtung des energieabhängigen, interstellaren
photoelektrischen Absorptionswirkungsquerschnittes
der energie- und feldwinkelabhängigen effektiven
Fläche des ROSAT-Detektors entspricht und die zweite Fläche die
Oberfläche des Neutronensterns repräsentiert.
Der Raum zwischen diesen beiden Objekten ist - entsprechend dem
interstellaren Medium - mit einem die Strahlung absorbierenden Gas
ausgefüllt, welches die vom Ort s abhängige Dichte nH(s)
besitzt und unter Beachtung des energieabhängigen, interstellaren
photoelektrischen Absorptionswirkungsquerschnittes 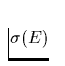 pro
Wasserstoffatom (Morison & McCammon 1983) durch die optische Dicke
pro
Wasserstoffatom (Morison & McCammon 1983) durch die optische Dicke
![]() dieses Gases beschrieben wird:
dieses Gases beschrieben wird:
Bezeichnet 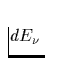 nun die infinitesimal kleine Strahlungsenergie
(Energiestrom innerhalb der umhüllenden Mantelfläche zwischen
Neutronenstern und Detektor), die der von der Photonenenergie und dem
Feldwinkel
nun die infinitesimal kleine Strahlungsenergie
(Energiestrom innerhalb der umhüllenden Mantelfläche zwischen
Neutronenstern und Detektor), die der von der Photonenenergie und dem
Feldwinkel ![]() abhängigen Detektorfläche
abhängigen Detektorfläche 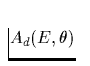 von der
im Abstand d befindlichen Sternoberfläche A* im Frequenzbereich
zwischen
von der
im Abstand d befindlichen Sternoberfläche A* im Frequenzbereich
zwischen ![]() und
und 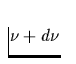 pro Sekunde zugestrahlt wird, so gilt:
pro Sekunde zugestrahlt wird, so gilt:
wobei 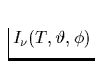 gemäß
gemäß ![$\,[I_\nu] =(\mbox{erg s}^{-1}\,
\mbox{cm}^{-2}\,\mbox{Hz}^{-1}\,\mbox{sr}^{-1})\,$](img196.gif) die pro Sekunde pro
Flächeneinheit und Raumwinkel im Frequenzbereich zwischen
die pro Sekunde pro
Flächeneinheit und Raumwinkel im Frequenzbereich zwischen ![]() und
und
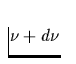 vom Stern in Richtung
vom Stern in Richtung 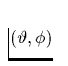 abgestrahlte
Intensität bezeichnet. Folgt die Energieverteilung der abgestrahlten
Photonen einem reinen Schwarzkörperspektrum, wie man es
näherungsweise für kühlende Neutronensterne erwartet, so ist die
emittierte Strahlung isotrop und die Intensität nur eine Funktion der
Temperatur allein. Das heißt, die von der strahlenden Fläche emittierte
Intensität stimmt mit der mittleren durch die Planck-Funktion
beschriebenen Strahlungsintensität der Quelle überein, und es
gilt
abgestrahlte
Intensität bezeichnet. Folgt die Energieverteilung der abgestrahlten
Photonen einem reinen Schwarzkörperspektrum, wie man es
näherungsweise für kühlende Neutronensterne erwartet, so ist die
emittierte Strahlung isotrop und die Intensität nur eine Funktion der
Temperatur allein. Das heißt, die von der strahlenden Fläche emittierte
Intensität stimmt mit der mittleren durch die Planck-Funktion
beschriebenen Strahlungsintensität der Quelle überein, und es
gilt![]() :
:
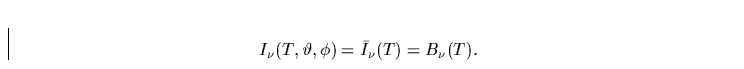 |
(7) |
Berücksichtigt man nun noch die aus der Strahlungstransportgleichung folgende exponentielle Abhängigkeit der Intensität von der optischen Dicke des durchstrahlten Mediums:
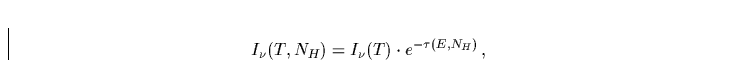 |
(8) |
worin 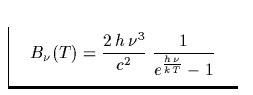 mit
mit ![$\textstyle\parbox{4cm}{\begin{displaymath}
\left[\; B_\nu(T)
\;\right] = \frac{\mbox{erg}}{\mbox{s cm}^2\,\mbox{Hz sr}}\end{displaymath}}$](img205.gif)
 die unabsorbierte Strahlungsintensität des Sterns pro Flächeneinheit,
Zeiteinheit, Raumwinkel
die unabsorbierte Strahlungsintensität des Sterns pro Flächeneinheit,
Zeiteinheit, Raumwinkel ![]() und Frequenzintervall
und Frequenzintervall ![]() bedeutet.
Da nun ein Photon gerade die Energiemenge
bedeutet.
Da nun ein Photon gerade die Energiemenge 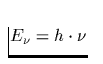 transportiert,
so sollte nach C.22 das Energiespektrum der Schwarzkörperstrahlung
am Detektor der folgenden Gleichung genügen:
transportiert,
so sollte nach C.22 das Energiespektrum der Schwarzkörperstrahlung
am Detektor der folgenden Gleichung genügen:
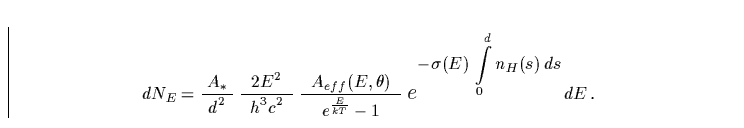 |
(9) |
Die Einflüsse der gravitativen Rotverschiebung auf die das Gravitationspotential des Neutronensterns verlassenden Photonen sind dabei gemäß den folgenden Gleichungen zu berücksichtigen:
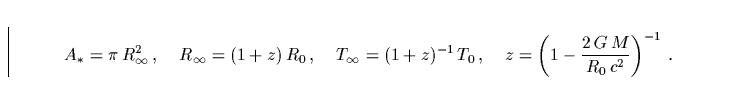
Integriert man nun Gleichung C.24 über den für den
ROSAT-PSPC- und HRI-Detektor zugänglichen Energiebereich von 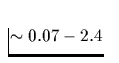 keV, so ergibt sich schließlich:
keV, so ergibt sich schließlich:
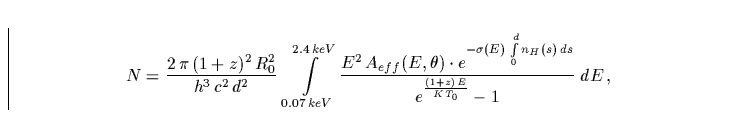 |
(10) |
also eine Gleichung, die bei Kenntnis der entsprechenden stellaren
Neutronensternparameter, wie Distanz ![]() und Säulendichte NH
sowie Sternmasse M und Neutronensternradius R0, die im
ROSAT-Energieband für kühlende Neutronensterne erwartete
Photonenzählrate liefert, sofern man für deren emittierte Strahlung ein
reines Schwarzkörperspektrum zugrunde legen kann.
Interessiert man sich dagegen für die Neutronensterntemperatur T0, die
einen gewissen Photonenfluß hervor ruft, so erhält man diesen Wert durch
Vorgabe von N und Iteration der Integralgleichung C.25.
und Säulendichte NH
sowie Sternmasse M und Neutronensternradius R0, die im
ROSAT-Energieband für kühlende Neutronensterne erwartete
Photonenzählrate liefert, sofern man für deren emittierte Strahlung ein
reines Schwarzkörperspektrum zugrunde legen kann.
Interessiert man sich dagegen für die Neutronensterntemperatur T0, die
einen gewissen Photonenfluß hervor ruft, so erhält man diesen Wert durch
Vorgabe von N und Iteration der Integralgleichung C.25.
Roberto Saglia