


Next: Linienensemble
Up: Die Linienstrahlungsbeschleunigung
Previous: Die Linienstrahlungsbeschleunigung
Betrachten wir zunächst den
Impulsübertrag durch die Absorption und Reemission von stellaren Photonen
in einer spektralen Linie (Übergangsfrequenz im atomaren System 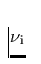 ),
wobei wir die endliche Profilbreite der Linie vernachlässigen wollen. Bei
diesem Prozess wird, pro Photon, ein radialer Impuls von
),
wobei wir die endliche Profilbreite der Linie vernachlässigen wollen. Bei
diesem Prozess wird, pro Photon, ein radialer Impuls von
| 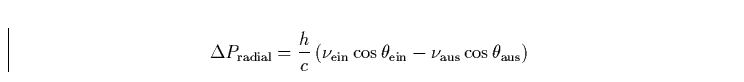 |
(1) |
vom absorbierten (``ein'') und reemittierten (``aus'') Photon auf das
absorbierende/ reemittierende Ion übertragen, wobei 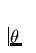 der
Winkel zwischen Richtung des Photons und radialem Einheitsvektor
(parallel zum Geschwindigkeitsvektor) ist, dem das Ion folgt.
der
Winkel zwischen Richtung des Photons und radialem Einheitsvektor
(parallel zum Geschwindigkeitsvektor) ist, dem das Ion folgt.
Aufgrund der gleichen Wahrscheinlichkeit, mit der nach innen bzw. nach
außen reemittiert wird, ist der Mittelwert
| 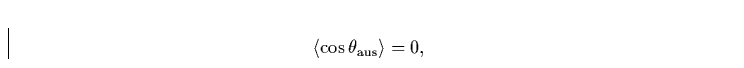 |
(2) |
während
| 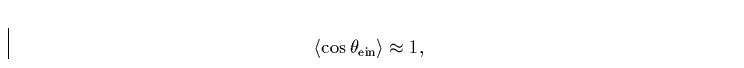 |
(3) |
da die Photonen vor der Wechselwirkung hauptsächlich aus Richtung des
Sternes kommen, d.h. parallel zum Geschwindigkeitsvektor propagieren.
Damit resultiert im Mittel
| 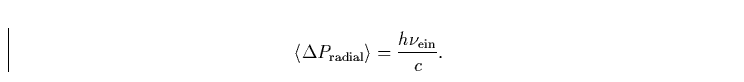 |
(4) |
Betrachten wir nun die in Abb. 13 skizzierte Situation, die den
Ausschnitt einer sphärischen Kugelschale (Geschwindigkeitszuwachs
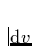 auf einer Skala
auf einer Skala 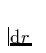 ) im Wind zeigt. (Photosphärische) Photonen
der Beobachterfrequenz = Startfrequenz
) im Wind zeigt. (Photosphärische) Photonen
der Beobachterfrequenz = Startfrequenz 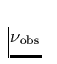 können immer dann von einem
Ion absorbiert werden, wenn ihre Frequenz im atomaren Bezugssystem
gleich der Übergangsfrequenz
können immer dann von einem
Ion absorbiert werden, wenn ihre Frequenz im atomaren Bezugssystem
gleich der Übergangsfrequenz 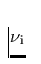 ist, d.h. aufgrund des Dopplereffektes
ist, d.h. aufgrund des Dopplereffektes
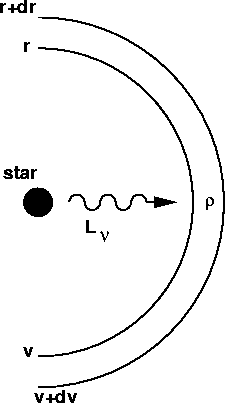
Abbildung:
Skizze eines blauen Überriesen, der seine eigene Windhülle bestrahlt.
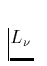 ist die spektrale Leuchtkraft bei Frequenz
ist die spektrale Leuchtkraft bei Frequenz
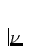 , v ist die Windgeschwindigkeit am Radius
r and
, v ist die Windgeschwindigkeit am Radius
r and 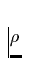 die dortige Dichte. Die eingezeichete Schale hat eine Masse
von
die dortige Dichte. Die eingezeichete Schale hat eine Masse
von 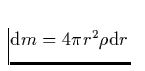 .
.
 |
gilt. Mit anderen Worten: Eine mögliche Absorption/Reemission, im
weiteren kurz ``Streuung'', bei höheren Geschwindigkeiten
erfordert Photonen, die auch bei höheren Frequenzen starten. Das
dem Geschwindigkeitsintervall 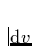 entsprechende Frequenzintervall
ergibt sich damit aus Gl. 5 als
entsprechende Frequenzintervall
ergibt sich damit aus Gl. 5 als
| 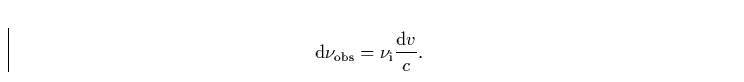 |
(5) |
Berechnen wir nun die Strahlungsbeschleunigung obiger Schale ``durch'' die
betrachtete Linie über die Definition jeglicher Beschleunigung, d.h.
| 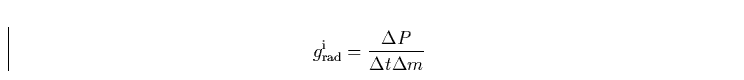 |
(6) |
so ergibt sich diese, wenn wir den Impulsübertrag durch eine einzelne
Streuung mit der Anzahl der im entsprechenden Frequenzintervall zur
Verfügung stehenden stellaren Photonen multiplizieren, und zwar
pro Zeiteinheit und Masse der beschleunigten Schale. Die Anzahl der Photonen
pro Zeiteinheit ist dabei
| 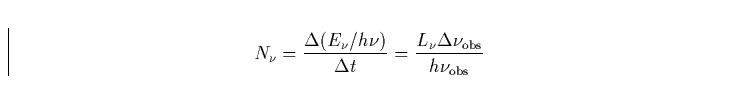 |
(7) |
wobei 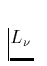 die stellare Leuchtkraft (= abgestrahlte Energie pro
Zeiteinheit) bei der Frequenz
die stellare Leuchtkraft (= abgestrahlte Energie pro
Zeiteinheit) bei der Frequenz 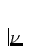 ist. Mit
ist. Mit 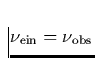 resultiert damit die (radiale) Beschleunigung der Massenschale durch eine
Linie
resultiert damit die (radiale) Beschleunigung der Massenschale durch eine
Linie
| 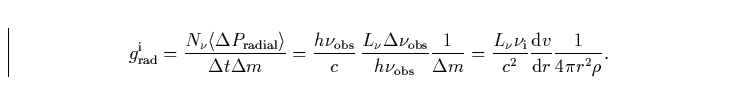 |
(8) |
Wir erhalten also das Ergebnis, daßdie Linenstrahlungsbeschleunigung
der Schale vom Geschwindigkeitsgradienten in der Schale abhängt!
(uff, Grübel, Grübel, ???) Eine sehr merkwürdige und in der Physik
wohl einmalige Abhängigkeit!
Bisher haben wir stillschweigend vorausgesetzt, daßalle Photonen,
die auf die fragliche Ionenspezies in der Schale treffen, tatsächlich
absorbiert werden. Dies mußnatürlich nicht immer so sein und trifft de
facto nur dann zu, wenn genügend viele Ionen vorhanden sind, die
absorbieren können. Mit anderen Worten: die
Wechselwirkungswahrscheinlichkeit (WWW, nicht zu verwechseln mit dem web)
wurde bisher mit ``1'' angesetzt, was zur Folge hatte, daßdie
Beschleunigung keinerlei Abhängigkeit von irgendwelchen atomaren
Eigenschaften aufwies, sondern nur von der Bestrahlung und der
hydrodynamischen Struktur abhing. Berücksichtigt man eine endliche WWW,
so ergibt sich diese als
| 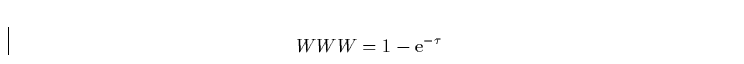 |
(9) |
wobei 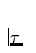 die optische Tiefe im betrachteten Übergang bei
die optische Tiefe im betrachteten Übergang bei 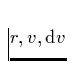 etc. ist (siehe unten). Aus dieser Eigenschaft lassen sich zwei Arten von
Linien herauskristallisieren. Für Linien mit
etc. ist (siehe unten). Aus dieser Eigenschaft lassen sich zwei Arten von
Linien herauskristallisieren. Für Linien mit 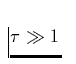 (d.h., sehr
vielen Ionen, sog. optisch dicken Linien) gilt
(d.h., sehr
vielen Ionen, sog. optisch dicken Linien) gilt 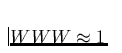 , während
optisch dünne Linien mit
, während
optisch dünne Linien mit 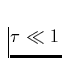 eine
eine 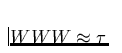 haben. Die
Strahlungsbeschleunigung einer optisch dünnen Linie ist also um den Faktor
haben. Die
Strahlungsbeschleunigung einer optisch dünnen Linie ist also um den Faktor
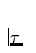 kleiner, als sie es im optisch dicken Fall wäre. Im weiteren werden
wir deshalb die (minore) Näherung verwenden, daßalle Linien mit
kleiner, als sie es im optisch dicken Fall wäre. Im weiteren werden
wir deshalb die (minore) Näherung verwenden, daßalle Linien mit 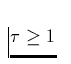 sich als optisch dick entsprechend Gl. 9 verhalten,
während Linien mit
sich als optisch dick entsprechend Gl. 9 verhalten,
während Linien mit 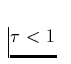 als optisch dünn definiert werden und ihre
Beschleunigung mit der aktuellen optischen Tiefe (die dann natürlich von
Details des Überganges abhängt) modifiziert wird. Man vergleiche den in
Kap. 4 geschilderten, analogen Unterschied zwischen gesättigten und
nicht-gesättigten P Cygni Profilen.
als optisch dünn definiert werden und ihre
Beschleunigung mit der aktuellen optischen Tiefe (die dann natürlich von
Details des Überganges abhängt) modifiziert wird. Man vergleiche den in
Kap. 4 geschilderten, analogen Unterschied zwischen gesättigten und
nicht-gesättigten P Cygni Profilen.



Next: Linienensemble
Up: Die Linienstrahlungsbeschleunigung
Previous: Die Linienstrahlungsbeschleunigung
Roberto Saglia
5/7/1998
![]()
![]()
![]()
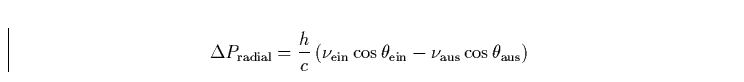
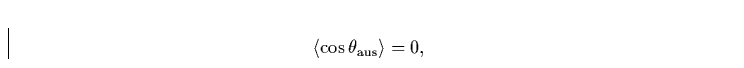
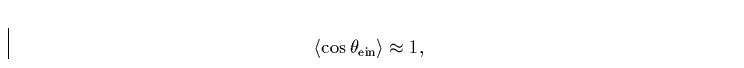
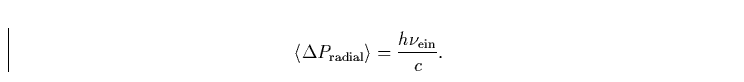
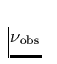 können immer dann von einem
Ion absorbiert werden, wenn ihre Frequenz im atomaren Bezugssystem
gleich der Übergangsfrequenz
können immer dann von einem
Ion absorbiert werden, wenn ihre Frequenz im atomaren Bezugssystem
gleich der Übergangsfrequenz 
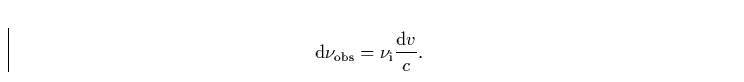
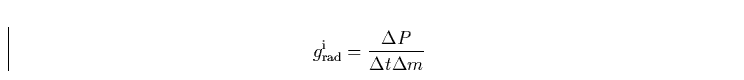
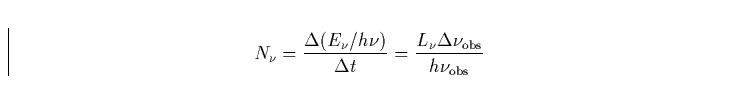
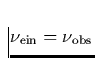 resultiert damit die (radiale) Beschleunigung der Massenschale durch eine
Linie
resultiert damit die (radiale) Beschleunigung der Massenschale durch eine
Linie
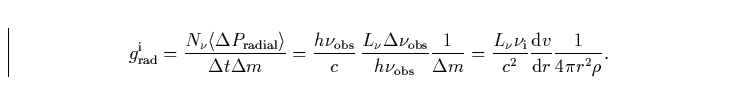
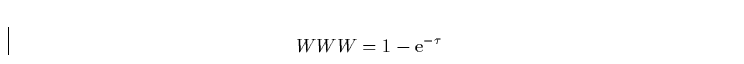
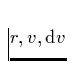 etc. ist (siehe unten). Aus dieser Eigenschaft lassen sich zwei Arten von
Linien herauskristallisieren. Für Linien mit
etc. ist (siehe unten). Aus dieser Eigenschaft lassen sich zwei Arten von
Linien herauskristallisieren. Für Linien mit 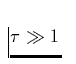 (d.h., sehr
vielen Ionen, sog. optisch dicken Linien) gilt
(d.h., sehr
vielen Ionen, sog. optisch dicken Linien) gilt 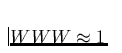 , während
optisch dünne Linien mit
, während
optisch dünne Linien mit 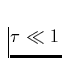 eine
eine 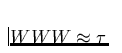 haben. Die
Strahlungsbeschleunigung einer optisch dünnen Linie ist also um den Faktor
haben. Die
Strahlungsbeschleunigung einer optisch dünnen Linie ist also um den Faktor
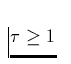 sich als optisch dick entsprechend Gl. 9 verhalten,
während Linien mit
sich als optisch dick entsprechend Gl. 9 verhalten,
während Linien mit 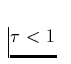 als optisch dünn definiert werden und ihre
Beschleunigung mit der aktuellen optischen Tiefe (die dann natürlich von
Details des Überganges abhängt) modifiziert wird. Man vergleiche den in
Kap. 4 geschilderten, analogen Unterschied zwischen gesättigten und
nicht-gesättigten P Cygni Profilen.
als optisch dünn definiert werden und ihre
Beschleunigung mit der aktuellen optischen Tiefe (die dann natürlich von
Details des Überganges abhängt) modifiziert wird. Man vergleiche den in
Kap. 4 geschilderten, analogen Unterschied zwischen gesättigten und
nicht-gesättigten P Cygni Profilen.