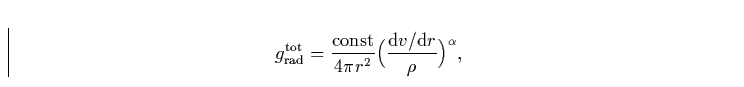Next: Lösung der Bewegungsgleichung
Up: Die Linienstrahlungsbeschleunigung
Previous: Impulsübertrag in einer Linie
Nun absorbiert natürlich nicht nur eine Linie, sondern eine (sehr) große
Zahl (etliche Millionen), wobei einige Zehntausend für die
Gesamtbeschleunigung 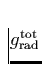 relevant sind. Um also diese zu berechnen,
müssen wir über alle einzelnen Beiträge summieren, und erhalten
relevant sind. Um also diese zu berechnen,
müssen wir über alle einzelnen Beiträge summieren, und erhalten
Die optische Tiefe der Linien läßt sich nun (im Rahmen einer gewissen
Näherung, der sog. ``Sobolev-'' oder Überschallnäherung) als
Funktion des Geschwindigkeitsgradienten, der Dichte und der sog.
Linienstärke ki angeben. (Eigentlich sollte ki dimensionslos
sein, deshalb treten in realiter noch zwei Normierungsgrößen auf - welche
könnten das sein? Aus Gründen der Vereinfachung begnügen wir uns aber
mit folgender Definition.)
| 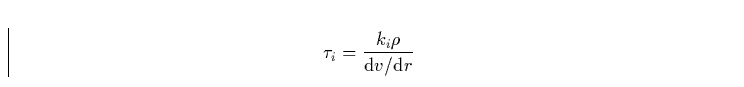 |
(10) |
Die wichtigste Eigenschaft der Linienstärke ist es, daßsie
alle atom- und plasmaphysikalischen Details des betreffenden Überganges
enthält, und für die meisten Linien praktisch konstant im Wind ist.
Aus obiger Definition ist sofort ersichtlich, daßder ``Grenzwert'' 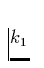 ,der optisch dünne von optisch dicken Linien separiert, nur von den
(lokalen) Windeigenschaften abhängt.
,der optisch dünne von optisch dicken Linien separiert, nur von den
(lokalen) Windeigenschaften abhängt.
| 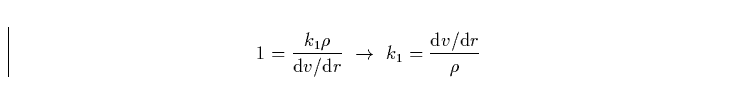 |
(11) |
Man beachte, daßalso 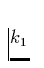 im Gegensatz zu ki im allgemeinen
über den Wind variieren wird. Unter Verwendung dieser Größe läßt sich
die gesamte Strahlungsbeschleunigung folgendermaßen schreiben:
im Gegensatz zu ki im allgemeinen
über den Wind variieren wird. Unter Verwendung dieser Größe läßt sich
die gesamte Strahlungsbeschleunigung folgendermaßen schreiben:
| 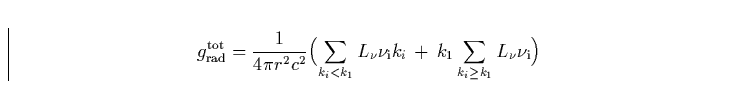 |
(12) |
Auch aus dieser Gleichung ist der Sättigungseffekt sofort ersichtlich:
optisch dicke Linien verhalten sich alle gleich, während optisch dünne
Linien entsprechend ihrer jeweiligen Linienstärke reagieren.
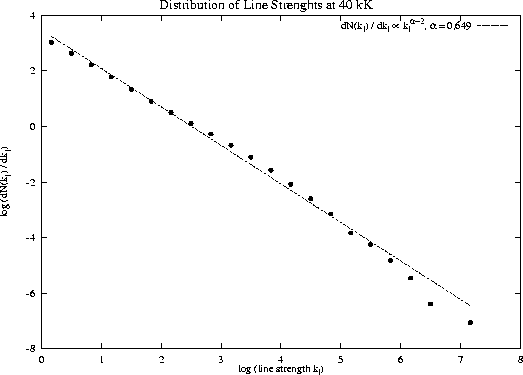
Abbildung:
Logarithmische Darstellung der Linienstärkenverteilungsfunktion eines
stellaren Windmodelles mit Teff=40000K. Gepunktet sind die Ergebnisse
aus einem Modellatmosphärencode, gestrichelt ein Potenzgesetzfit
entsprechend Gl. 15.
 |
Die gesamte bisherige Vorgehensweise nützt uns bisher nicht allzu viel, da
wir immer noch die Linienstärken der optisch dünnen Linien benötigen.
Für das weitere Vorgehen kommt uns nun jedoch ein interessantes Faktum
zu Hilfe, das nicht unmittelbar einsichtig ist und hier nur angegeben wird:
Betrachtet man ein großes Ensemble von Linien, so genügen diese Linien
bzgl. ihrer Stärke einer einfachen Statistik (vgl. Abb. 14):
Die Anzahl der Linien in einem Frequenzintervall
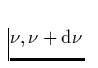 mit Linienstärken
mit Linienstärken
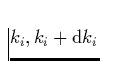 kann durch ein Potenzgesetz beschrieben werden
kann durch ein Potenzgesetz beschrieben werden
| 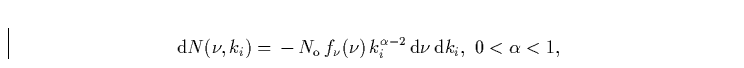 |
(13) |
wobei die Frequenzverteilung unabhängig von der
Linienstärkenverteilung ist! (Die bislang unterdrückten Dimensionen
werden in 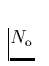 mitberücksichtigt.) Ersetzt man nun in Gl. 14 die
Summen durch entsprechende Doppelintegrale und verwendet (15),
so findet man
mitberücksichtigt.) Ersetzt man nun in Gl. 14 die
Summen durch entsprechende Doppelintegrale und verwendet (15),
so findet man
Die zweite Gleichung zeigt zwei Punkte auf: Sowohl die optisch dicke als
auch die optisch dünne Linienbeschleunigung skalieren mit der gleichen
Potenz 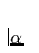 , und das Verhältnis dieser Beschleunigungen ist
durch
, und das Verhältnis dieser Beschleunigungen ist
durch 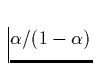 gegeben, entspricht also bei einem Wert von
gegeben, entspricht also bei einem Wert von
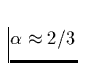 (Vgl. Abb. 14) einem Faktor 2!
(Vgl. Abb. 14) einem Faktor 2!
Unser ENDERGEBNIS für die Linienbeschleunigung läßt sich also
folgendermaßen formulieren:
| 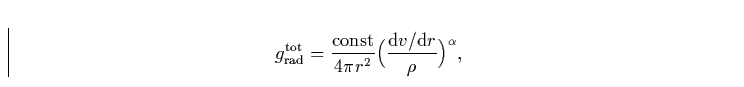 |
(14) |
und hängt, bis auf die Normierungskonstante und den Exponenten, nur noch
von hydrodynamischen Größen ab. (Die wahre Kunst der Windrechnungen ist
es jedoch, gerade diese beiden Größen, in die die Besetzungszahlen
aller beitragenden Ionen eingehen, konsistent zu berechnen!)



Next: Lösung der Bewegungsgleichung
Up: Die Linienstrahlungsbeschleunigung
Previous: Impulsübertrag in einer Linie
Roberto Saglia
5/7/1998
![]()
![]()
![]()
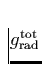 relevant sind. Um also diese zu berechnen,
müssen wir über alle einzelnen Beiträge summieren, und erhalten
relevant sind. Um also diese zu berechnen,
müssen wir über alle einzelnen Beiträge summieren, und erhalten
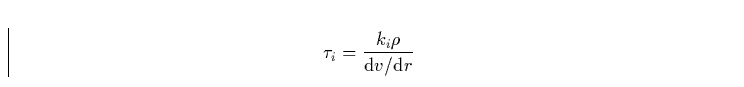
![]() ,der optisch dünne von optisch dicken Linien separiert, nur von den
(lokalen) Windeigenschaften abhängt.
,der optisch dünne von optisch dicken Linien separiert, nur von den
(lokalen) Windeigenschaften abhängt.
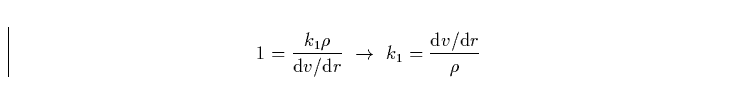
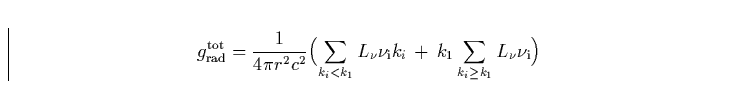

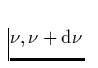 mit Linienstärken
mit Linienstärken
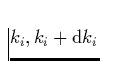 kann durch ein Potenzgesetz beschrieben werden
kann durch ein Potenzgesetz beschrieben werden
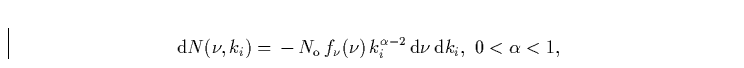
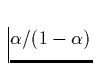 gegeben, entspricht also bei einem Wert von
gegeben, entspricht also bei einem Wert von
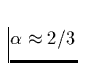 (Vgl. Abb. 14) einem Faktor 2!
(Vgl. Abb. 14) einem Faktor 2!