Next: Die Windimpuls-Leuchtkraft-Relation (WLR) Up: Theorie strahlungsdruckgetriebener Winde - Previous: Linienensemble
![]()
![]()
![]()
Next: Die Windimpuls-Leuchtkraft-Relation (WLR)
Up: Theorie strahlungsdruckgetriebener Winde -
Previous: Linienensemble
Nachdem wir nun einen (relativ einfachen) Ausdruck für die Linienbeschleunigung gefunden haben, können wir uns daran machen, die hydrodynamische Struktur des Windes zu untersuchen. Dabei gilt es, folgende hydrodynamische Gleichungen (für stationäre, sphärisch-symmetrische Strömungen) zu berücksichtigen:
1. Die Kontinuitätsgl.:  ,
,
2. die Impulsgl.:  ,
,
3. die Zustandsgl: 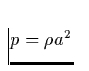 ,
,
wobei p der Druck, a die isotherme Schallgeschwindigkeit, 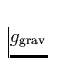 die Schwerebeschleunigung des Sternes und
die Schwerebeschleunigung des Sternes und ![]() das Verhältnis von
Thomsonsbeschleunigung (Strahlungsbeschleunigung aufgrund der Streuung von
Photonen an freien Elektronen,
das Verhältnis von
Thomsonsbeschleunigung (Strahlungsbeschleunigung aufgrund der Streuung von
Photonen an freien Elektronen, 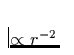 ) und Schwerebeschleunigung
ist. Man beachete:
) und Schwerebeschleunigung
ist. Man beachete: 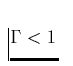 für stabile Sterne,
für stabile Sterne, 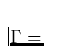 O[0.5] für
Überriesen.
O[0.5] für
Überriesen.
Diese Gleichungen wollen wir nun für den Überschallbereich des Windes lösen. In diesem Bereich lassen sich die Druckkräfte vernachlässigen (warum?), und wir finden unter Verwendung der Kontinuitätsgleichung und (17) die Bewegungsgleichung des Windes im Überschallbereich:
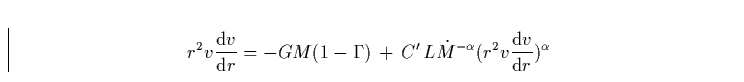 |
(15) |
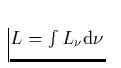 und Konstante C'. (Wie lautet C'?)
und Konstante C'. (Wie lautet C'?)
Obige Gleichung läßt sich unter Verwendung der Variablen 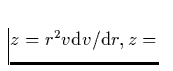 const, (alle anderen Größen konstant)
einfach lösen (z.B. graphisch), und wir finden nur dann eine eindeutige
Lösung für die Massenverlustrate, falls gilt:
const, (alle anderen Größen konstant)
einfach lösen (z.B. graphisch), und wir finden nur dann eine eindeutige
Lösung für die Massenverlustrate, falls gilt:
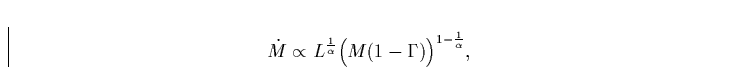 |
(16) |
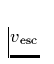 .
.
Wie gesagt, ist die gesamte obige Ableitung in einigen Teilen stark
vereinfacht. Zieht man jedoch die Analyse vollständig durch (die
entsprechenden Verfeinerungen werden im Praktikum besprochen), so
ergeben sich keine gravierenden Änderungen. So bleibt die
Skalierungsrelation für ![]() vollständig erhalten, und auch an der
Proportionalität
vollständig erhalten, und auch an der
Proportionalität 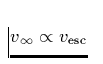 ändert sich nichts. (Nur die
Proportionalitätskonstante ist verschieden). Die wichtigste Änderung
betrifft die Form des Geschwindigkeitsfeldes. Der Exponent 1/2
ist nicht mehr länger gültig, sondern
ändert sich nichts. (Nur die
Proportionalitätskonstante ist verschieden). Die wichtigste Änderung
betrifft die Form des Geschwindigkeitsfeldes. Der Exponent 1/2
ist nicht mehr länger gültig, sondern
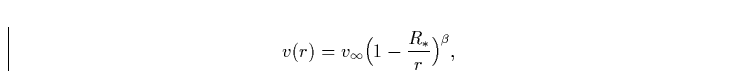 |
(17) |
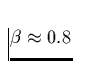 . Dieser Exponent
. Dieser Exponent
Roberto Saglia