Next: Analyse von UV P Up: Theorie strahlungsdruckgetriebener Winde - Previous: Lösung der Bewegungsgleichung
![]()
![]()
![]()
Next: Analyse von UV P
Up: Theorie strahlungsdruckgetriebener Winde -
Previous: Lösung der Bewegungsgleichung
Obige Skalierungsrelationen machen nun die Existenz der sog.
Windimpuls-Leuchtkraft-Relation (WLR), die erstmals von Kudritzki et al.
![]() rein empirisch gefunden wurde, auch von einem theoretischen
Aspekt her einsichtig. Die ``beobachtete'' WLR für galaktische Überriesen
(die Sie im Rahmen des Praktikums ableiten sollen), liest sich
folgendermaßen:
rein empirisch gefunden wurde, auch von einem theoretischen
Aspekt her einsichtig. Die ``beobachtete'' WLR für galaktische Überriesen
(die Sie im Rahmen des Praktikums ableiten sollen), liest sich
folgendermaßen:
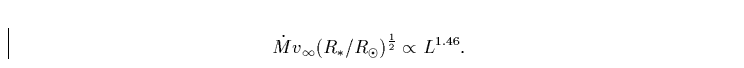 |
(18) |
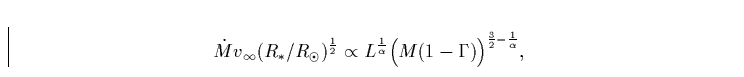 |
(19) |
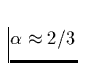 , so sehen wir, daßdiese Abhängigkeit fast
vollständig verschwindet, in Übereinstimmung mit dem empirischen
Resultat, was einem
, so sehen wir, daßdiese Abhängigkeit fast
vollständig verschwindet, in Übereinstimmung mit dem empirischen
Resultat, was einem Letztlich stellt sich noch die Frage, wie diese WLR tatsächlich genutzt werden soll. Derzeit sind Mitarbeiter der Heißsterngruppe unseres Institutes u.a. damit beschäftigt, bei Objekten mit bekannter Entfernung und in Abhängigkeit vom ``Metallgehalt'' der Winde (Warum diese Abhängigkeit?), entsprechende empirische Relationen zu erstellen, u.zw. auf die gleiche Weise, wie es in diesem Versuch für galaktische O-Überriesen gemacht werden soll. Hat man einmal solche Relationen und kennt den Metallgehalt des Sternes (aus einer detaillierten Liniendiagnostik), so läßt sich seine Entfernung in folgender Weise bestimmen:
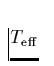 des Sternes wird über photosphärischen Analysen
abgeleitet.
des Sternes wird über photosphärischen Analysen
abgeleitet.
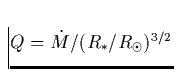 (vgl. Kap. 7.2) bestimmt.
(vgl. Kap. 7.2) bestimmt.
Wenn die (für die entsprechende Metallizität) gültige WLR
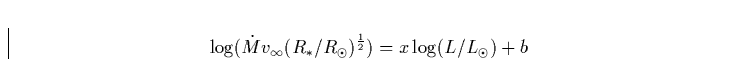 |
(20) |
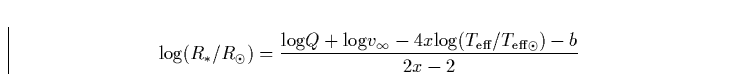 |
(21) |
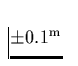 angegeben werden
kann. Damit ist diese neuartige
Vorgehensweise mindestens genauso gut wie herkömmliche Methoden
(hauptsächlich: Periode-Leuchtkraft-Relation von Cepheiden) und wird
eine unabhängige Bestimmung von Entfernungen auf ``mittleren''
Skalen und damit eine weitere Eichung der Hubble-Konstanten ermöglichen.
angegeben werden
kann. Damit ist diese neuartige
Vorgehensweise mindestens genauso gut wie herkömmliche Methoden
(hauptsächlich: Periode-Leuchtkraft-Relation von Cepheiden) und wird
eine unabhängige Bestimmung von Entfernungen auf ``mittleren''
Skalen und damit eine weitere Eichung der Hubble-Konstanten ermöglichen.
Roberto Saglia