Next: Analyse des H-Profiles Up: Gebrauchsanleitung Previous: Die Windimpuls-Leuchtkraft-Relation (WLR)
![]()
![]()
![]()
Next: Analyse des H-Profiles
Up: Gebrauchsanleitung
Previous: Die Windimpuls-Leuchtkraft-Relation (WLR)
Aus den im Praktikumsversuch gefitteten UV-Profilen ergeben sich, neben der
Meßgrößen 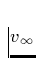 , auch Werte, die den Verlauf der Linienopazität und
damit der entsprechenden Besetzungszahlen repräsentieren. Insbesondere in
Fällen, in denen das Profil nicht gesättigt ist, lassen sich daraus
interessante Größen ableiten und mit theoretischen Vorhersagen
vergleichen. Die entsprechenden Variablen seien (wie im zu verwendenden
Fit-Programm) k und
, auch Werte, die den Verlauf der Linienopazität und
damit der entsprechenden Besetzungszahlen repräsentieren. Insbesondere in
Fällen, in denen das Profil nicht gesättigt ist, lassen sich daraus
interessante Größen ableiten und mit theoretischen Vorhersagen
vergleichen. Die entsprechenden Variablen seien (wie im zu verwendenden
Fit-Programm) k und ![]() genannt (nicht zu verwechseln mit den
Größen gleichen Namens aus Kap. 5), und wir werden im folgenden zeigen,
wie diese Größen mit tatsächlichen physikalischen Parametern des Windes
zusammenhängen.
genannt (nicht zu verwechseln mit den
Größen gleichen Namens aus Kap. 5), und wir werden im folgenden zeigen,
wie diese Größen mit tatsächlichen physikalischen Parametern des Windes
zusammenhängen.
Parametrisiert man nämlich die Besetzungszahldichte nl(r) des unteren
absorbierenden Niveaus des Übergangs über die Dichte und die
Elementhäufigkeiten, kann man aus dem Linienprofil Information über das
Produkt aus Massenverlustrate ![]() und Ionisationsgrad X(v)
gewinnen.
und Ionisationsgrad X(v)
gewinnen.
Die in Gl. 12 eingeführte optische Tiefe der betrachteten Linie läßt sich auch folgendermaßen schreiben, wenn wir von nun an Geschwindigkeiten in Einheiten der Endgeschwindigkeit und Radien in Einheiten des stellaren Radius messen
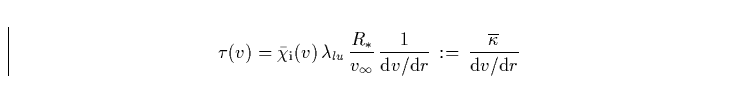 |
(22) |
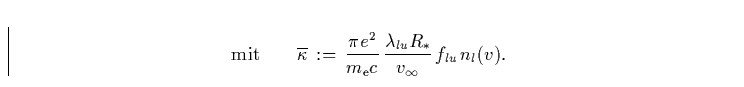 |
(23) |
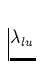 die Wellenlänge des betrachteten Überganges. In der Definition von
die Wellenlänge des betrachteten Überganges. In der Definition von
Die Besetzungszahldichte nljk des Levels l in der Ionisationsstufe
j von Element k kann über den Anregungsgrad E, den Ionisationsgrad X
und die relative Häufigkeit ![]() des Elements bezüglich Wasserstoff
ausgedrückt werden:
des Elements bezüglich Wasserstoff
ausgedrückt werden:
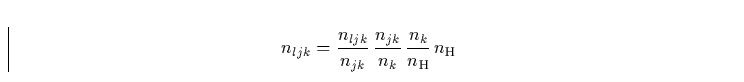 |
(24) |
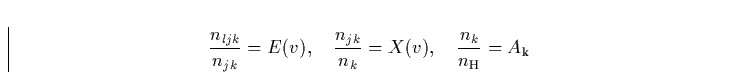
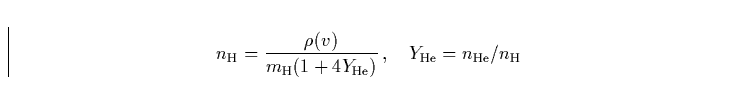 |
(25) |
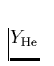 ist die relative Häufigkeit von Helium zu Wasserstoff,
ist die relative Häufigkeit von Helium zu Wasserstoff,
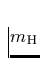 ist die Masse des H-Atoms. Die Dichte
ist die Masse des H-Atoms. Die Dichte 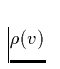 erhält man aus der
schon eingeführten Kontinuitätsgleichung:
erhält man aus der
schon eingeführten Kontinuitätsgleichung:
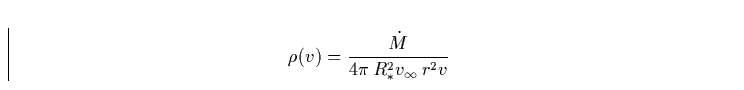
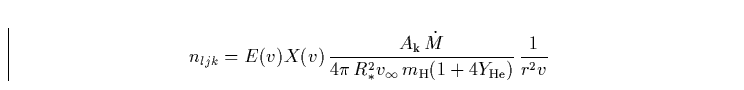 |
(26) |
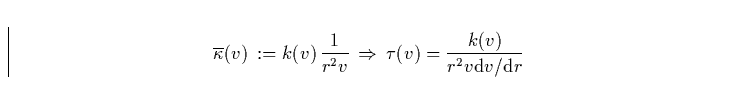 |
(27) |
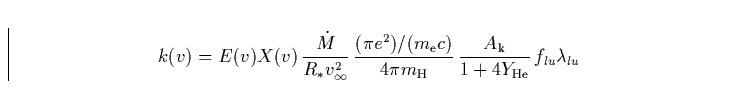 |
(28) |
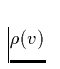 . Im weiteren können wir E(v) = 1 setzen,
da wir uns in diesem Praktikum nur mit den sog. Resonanzlinien von NV
und CIV beschäftigen werden, die beide vom Grundzustand ausgehen und
deren Besetzungszahl demzufolge in etwa derjenigen der gesamten
Ionisationsstufe entspricht. Unter dieser Bedingung ist k(v) direkt
proportional dem Ionisationsverlauf X(v):
. Im weiteren können wir E(v) = 1 setzen,
da wir uns in diesem Praktikum nur mit den sog. Resonanzlinien von NV
und CIV beschäftigen werden, die beide vom Grundzustand ausgehen und
deren Besetzungszahl demzufolge in etwa derjenigen der gesamten
Ionisationsstufe entspricht. Unter dieser Bedingung ist k(v) direkt
proportional dem Ionisationsverlauf X(v):
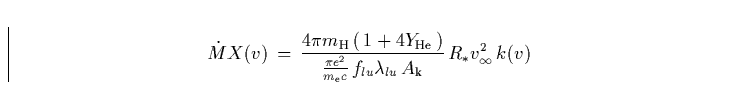 |
(29) |
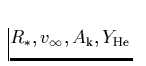 ) sind meistens in
vergleichsweise guter Genauigkeit beschaffbar. Der Wert für X ist jedoch
nicht mit einer empirischen Analysemethode ausschließlich unter Verwendung
der UV-Spektren bestimmbar. Dies erfordert entweder ein numerisches
Atmosphärenmodell oder er kann nur ermittelt werden,
wenn die Massenverlustrate bereits anderweitig bestimmt worden ist (z.B aus der
H
) sind meistens in
vergleichsweise guter Genauigkeit beschaffbar. Der Wert für X ist jedoch
nicht mit einer empirischen Analysemethode ausschließlich unter Verwendung
der UV-Spektren bestimmbar. Dies erfordert entweder ein numerisches
Atmosphärenmodell oder er kann nur ermittelt werden,
wenn die Massenverlustrate bereits anderweitig bestimmt worden ist (z.B aus der
H
Eine häufig verwendete Größe, die direkt aus den Linienfits ableitbar
ist, ist die Säulendichte 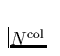 der Absorber (in cm-2) zwischen zwei
Positionen im Wind:
der Absorber (in cm-2) zwischen zwei
Positionen im Wind:
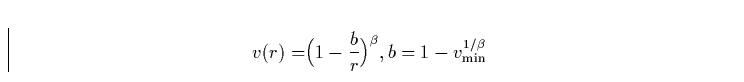 |
(30) |
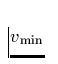 haben
soll, die in der Größenordung der Schallgeschwindigkeit (
haben
soll, die in der Größenordung der Schallgeschwindigkeit (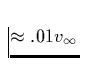 ) liegt. Mit dieser Vorgehensweise wird berücksichtigt,
daßunterhalb des Schallpunktes die Druckterme dominieren, so daßdas
) liegt. Mit dieser Vorgehensweise wird berücksichtigt,
daßunterhalb des Schallpunktes die Druckterme dominieren, so daßdas
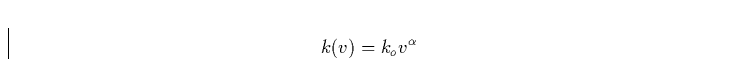 |
(31) |
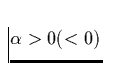 einen
nach innen abfallenden (bzw. ansteigenden) Ionisationsgrad andeutet.
einen
nach innen abfallenden (bzw. ansteigenden) Ionisationsgrad andeutet.
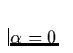 bedeutet natürlich konstante Ionisation.
bedeutet natürlich konstante Ionisation.
Mit diesen Definitionen (35,36) und den aus dem
Fitprogramm bestimmten Größen 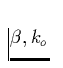 und
und ![]() läßt sich
die Säulendichte (34) abschätzen:
läßt sich
die Säulendichte (34) abschätzen:
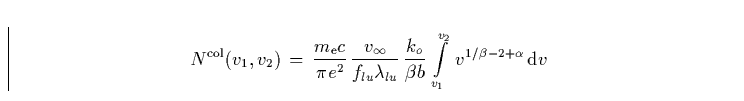 |
(32) |
Definiert man jetzt einen ,,mittleren Ionisationsgrad`` ![]() als das
Verhältnis der Anzahl aller Ionen eines Elements in der Säule
zur Gesamtzahl der Teilchen des Elements, dann erhält man:
als das
Verhältnis der Anzahl aller Ionen eines Elements in der Säule
zur Gesamtzahl der Teilchen des Elements, dann erhält man:
Roberto Saglia