Next: H-Profil und Massenverlustrate Up: Analyse des H-Profiles Previous: Analyse des H-Profiles
![]()
![]()
![]()
Next: H-Profil und Massenverlustrate
Up: Analyse des H-Profiles
Previous: Analyse des H-Profiles
Das Zusammentreffen dreier günstiger Umstände ist dafür die Ursache:
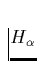 -Linie ist eine sogenannte
-Linie ist eine sogenannte 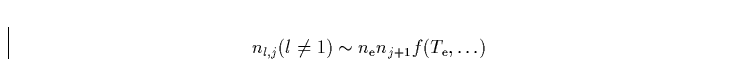 |
(33) |
Aus dieser Tatsache folgt u.a., daßdas Verhältnis von Emissions- und
Absorptionskoeffizient, die sog. Linienquellfunktion ![]() (die im
wesentlichen vom Verhältnis der Besetzungszahlen des oberen und unteren
Niveaus des Linienüberganges bestimmt wird), für Linienübergänge
oberhalb des Grundzustandes relativ konstant bleibt, solange dies auch für
die Elektronentemperatur
(die im
wesentlichen vom Verhältnis der Besetzungszahlen des oberen und unteren
Niveaus des Linienüberganges bestimmt wird), für Linienübergänge
oberhalb des Grundzustandes relativ konstant bleibt, solange dies auch für
die Elektronentemperatur 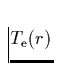 gilt. In guter Näherung entspricht
die Linienquellfunktion dann der Planckfunktion
gilt. In guter Näherung entspricht
die Linienquellfunktion dann der Planckfunktion
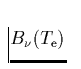 . Verständlich wird dieses Verhalten dadurch, daßdie
Population dieser angeregten Niveaus hauptsächlich durch die
Strahlungsrekombination (Elektron + Ion(j+1) + Photon
. Verständlich wird dieses Verhalten dadurch, daßdie
Population dieser angeregten Niveaus hauptsächlich durch die
Strahlungsrekombination (Elektron + Ion(j+1) + Photon ![]() angeregtes
Ion(j), gefolgt von einer Abregungskaskade nach unten) gefüttert wird, die
aufgrund der (Maxwellschen) Geschwindigkeitsverteilung von Elektronen und
Ionen ein thermischer Prozess ist.
angeregtes
Ion(j), gefolgt von einer Abregungskaskade nach unten) gefüttert wird, die
aufgrund der (Maxwellschen) Geschwindigkeitsverteilung von Elektronen und
Ionen ein thermischer Prozess ist.
Für die im vorhergehenden Kapitel angesprochenen Resonanzlinien gilt
hingegen 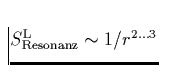 . Dies liegt im
wesentlichen daran, daßdiese Linien nur eine (Quasi-)Streuung der
Photonen bewirken, d.h. sich die Anzahl der vorhandenen Photonen mit dem
anwachsenden Windvolumen verdünnt.
. Dies liegt im
wesentlichen daran, daßdiese Linien nur eine (Quasi-)Streuung der
Photonen bewirken, d.h. sich die Anzahl der vorhandenen Photonen mit dem
anwachsenden Windvolumen verdünnt.
Wie wir weiter unten sehen werden, ist es gerade diese Konstanz der
H![]() -Linienquellfunktion, die den signifikanten Unterschied der Form
des H
-Linienquellfunktion, die den signifikanten Unterschied der Form
des H![]() -Linienprofiles gegenüber einem P Cygni Profil bewirkt; man
vergleiche die beiden Profile auf dem Titelbild dieser
Anleitung
-Linienprofiles gegenüber einem P Cygni Profil bewirkt; man
vergleiche die beiden Profile auf dem Titelbild dieser
Anleitung![]() .
.
Handelt es sich schließlich bei der Ionisationsstufe (j+1) um die Hauptionsationsstufe (wie es z.B. bei heißen Sternen für HII der Fall ist), gilt damit im wesentlichen
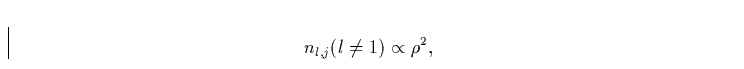 |
(34) |
und aus 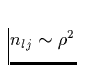 folgt damit auch, daßdie
Opazität ein analoges Verhalten
folgt damit auch, daßdie
Opazität ein analoges Verhalten 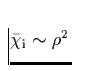 aufweist.
aufweist.
In Sternwinden treten solche sog. Rekombinationslinien bei zunehmender
Winddichte in Emission auf, wobei die Äquivalentbreite proportional zum
Quadrat der Winddichte ist (genauer gesagt zu 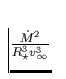 , vgl. Gl. 41);
sie sind daher bessere
, vgl. Gl. 41);
sie sind daher bessere ![]() -Indikatoren als Resonanzlinien, zumindest
solange die Winddichte nicht zu gering ist!
-Indikatoren als Resonanzlinien, zumindest
solange die Winddichte nicht zu gering ist!
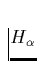 ist eine der stärksten Linien.
ist eine der stärksten Linien.
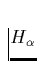 -Linie.
-Linie.
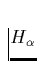 ist gut verstanden.
ist gut verstanden.
Roberto Saglia