Next: Durchführung des Versuches Up: Analyse des H-Profiles Previous: Warum H?
![]()
![]()
![]()
Next: Durchführung des Versuches
Up: Analyse des H-Profiles
Previous: Warum H?
Im folgenden wird der Zusammenhang zwischen
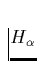 -Profil und Massenverlustrate
dargestellt. Wir verwenden dazu die gleiche (Sobolev-)Näherung wie auch
schon in früheren Kapiteln, um die optische Tiefe des Linienüberganges
zu berechnen.
-Profil und Massenverlustrate
dargestellt. Wir verwenden dazu die gleiche (Sobolev-)Näherung wie auch
schon in früheren Kapiteln, um die optische Tiefe des Linienüberganges
zu berechnen.
Ebenso vernachlässigen wir bei der Abschätzung des Produktes 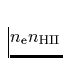 den geringen Metallgehalt (s.o., obwohl die Metallinien den Wind
beschleunigen) und berücksichtigen nur die Elemente H und He.
Schließlich sind diese beiden Elemente bei O-Sternen fast vollständig
ionisiert:
den geringen Metallgehalt (s.o., obwohl die Metallinien den Wind
beschleunigen) und berücksichtigen nur die Elemente H und He.
Schließlich sind diese beiden Elemente bei O-Sternen fast vollständig
ionisiert:
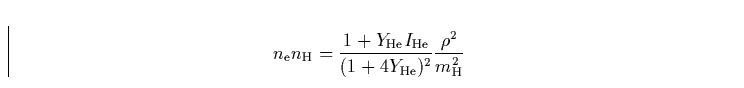 |
(35) |
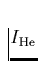 : Anzahl freier Elektronen pro Heliumatom = 2 unter den
geschilderten Bedingungen). Analog zu Gl. 26 lautet
die optische Tiefe
: Anzahl freier Elektronen pro Heliumatom = 2 unter den
geschilderten Bedingungen). Analog zu Gl. 26 lautet
die optische Tiefe
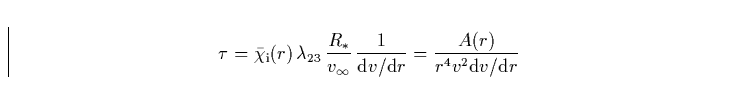 |
(36) |
Unter Verwendung der Saha-Boltzmanngleichung, der Kontinuitätsgleichung, Gl. (41, 42) und der atomaren Konstanten des Überganges finden wir für die Größe A(r)
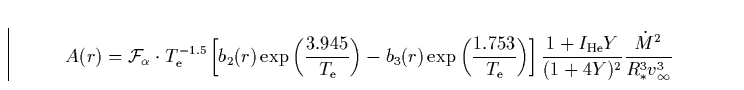 |
(37) |
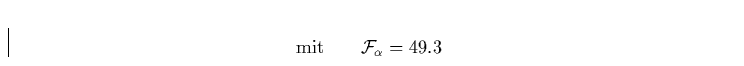
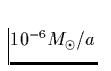 ,
, 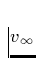 in 1000 km/s,
in 1000 km/s, 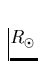 und
und 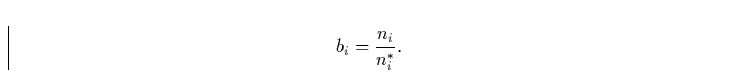 |
(38) |
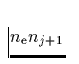 , die aktuellen NLTE
, die aktuellen NLTE
Gl. 43 zeigt den grundsätzlichen Unterschied der
Skalierungsrelationen zwischen Resonanz- und Rekombinationslinien sofort
auf. Während die optische Tiefe von Resonanzlinien von der Kombination
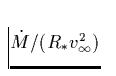 abhängt (vgl. 32), finden wir hier aufgrund
der zusätzlichen
abhängt (vgl. 32), finden wir hier aufgrund
der zusätzlichen ![]() -Abhängigkeit eine Funktion von
-Abhängigkeit eine Funktion von
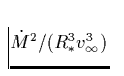 !
!
Bei bekannter Endgeschwindigkeit sollten sich also (synthetische) H![]() -Profile
kaum verändern, solange die Größe
-Profile
kaum verändern, solange die Größe 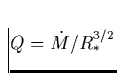 unverändert
bleibt. Dies ist der Grund, warum wir in Kap. 5.3 diese Kombination als
eigentliche Meßgröße angeführt haben.
unverändert
bleibt. Dies ist der Grund, warum wir in Kap. 5.3 diese Kombination als
eigentliche Meßgröße angeführt haben.
Der Windparameter A bewegt sich für OB-Sterne typischerweise im
Wertebereich zwischen 10-7 und 10-1, so daß die
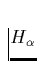 -Linie im größten Teil des Windes optisch dünn ist (vgl.
(42)). Man kann davon ausgehen, daß auch das Kontinuum in diesem
Bereich optisch dünn ist. Bei der Berechnung des Profiles kann daher in
guter Näherung der Beitrag des Kontinuums zur Quellfunktion vernachlässigt
werden; berücksichtigt wird nur die Linienquellfunktion
-Linie im größten Teil des Windes optisch dünn ist (vgl.
(42)). Man kann davon ausgehen, daß auch das Kontinuum in diesem
Bereich optisch dünn ist. Bei der Berechnung des Profiles kann daher in
guter Näherung der Beitrag des Kontinuums zur Quellfunktion vernachlässigt
werden; berücksichtigt wird nur die Linienquellfunktion 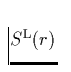 .Letztendlich ergibt sich das H
.Letztendlich ergibt sich das H![]() -Profil (in Einheiten des Kontinuums) in
Sobolev-Näherung wie folgt:
-Profil (in Einheiten des Kontinuums) in
Sobolev-Näherung wie folgt:
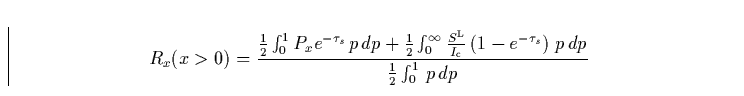 |
(39) |
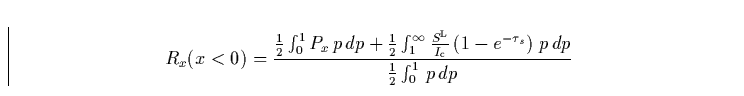 |
(40) |
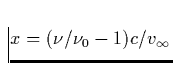 , Px : photosphärisches
Profil,
, Px : photosphärisches
Profil, 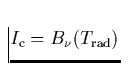 Kontinuumsintensität bei x=0
(Linienmitte)).
Das Kontinuum
Kontinuumsintensität bei x=0
(Linienmitte)).
Das Kontinuum 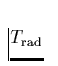 die entsprechende photosphärische Strahlungstemperatur ist.
die entsprechende photosphärische Strahlungstemperatur ist.
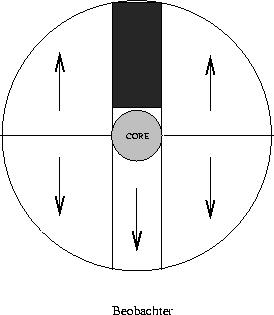 |
Die Interpretation dieser Gleichungen im Zusammenspiel mit Abb. 15
ist analog zu der in Abb. 11 skizzierten Entstehung eines P Cygni
Profiles. Der wesentliche Unterschied ist hier der stärkere Abfall von
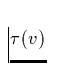 nach außen, im Gegensatz zur Quellfunktion, die praktisch
konstant bleibt. Der blaue Teil des Profiles Rx(x>0) wird wiederum
durch dasjenige Material verursacht, das auf den Beobachter zukommt bzw.
durch Photonen, die vom Stern abgestrahlt werden. Vor der Sternscheibe sieht
man das photosphärische H
nach außen, im Gegensatz zur Quellfunktion, die praktisch
konstant bleibt. Der blaue Teil des Profiles Rx(x>0) wird wiederum
durch dasjenige Material verursacht, das auf den Beobachter zukommt bzw.
durch Photonen, die vom Stern abgestrahlt werden. Vor der Sternscheibe sieht
man das photosphärische H![]() -Profil Px, das vom Wind geschwächt
wird. Die Emission stammt vom zweiten Integral, dessen Beitrag umso
größer ist, je größer die emittierende Fläche ist, d.h. maximal bei
x=0 ist und minimal dort, wo
-Profil Px, das vom Wind geschwächt
wird. Die Emission stammt vom zweiten Integral, dessen Beitrag umso
größer ist, je größer die emittierende Fläche ist, d.h. maximal bei
x=0 ist und minimal dort, wo ![]() praktisch verschwindet. Die
größtmögliche Breite des Profiles ist wiederum bei x=1 entsprechend
praktisch verschwindet. Die
größtmögliche Breite des Profiles ist wiederum bei x=1 entsprechend
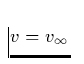 gegeben.
gegeben.
Auf der roten Seite des Profiles Rx(x<0) sieht man zum einen das ungeschwächte photosphärische Profil, da bei diesen Frequenzen der Wind vor der Sternscheibe NICHT absorbieren kann. Man sieht hier nur den hinteren Wind, wobei sein Beitrag (2. Integral) symmetrisch zum blauen Anteil ist.
Auf diese Weise wird die Variation des H![]() -Profiles mit anwachsender
Massenverlustrate klar. Bei kleinem
-Profiles mit anwachsender
Massenverlustrate klar. Bei kleinem ![]() und entsprechend niedrigem
und entsprechend niedrigem
![]() dominieren jeweils die beiden ersten Integrale,
dominieren jeweils die beiden ersten Integrale, 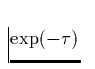 ist
klein und wir sehen ein symmetrisches photosphärisches Profil. Wächst
ist
klein und wir sehen ein symmetrisches photosphärisches Profil. Wächst
![]() an, fangen die beiden zweiten Integrale an, merklich beitzutragen,
und das photosphärische Profil wird langsam aufgefüllt, wobei das
Resultat aufgrund der Asymmetrie des ersten Anteils ein asymmetrisches Profil
ergibt. Bei sehr hohen Massenverlustraten dominiert schließlich der zweite
Term vollständig, und wir erhalten ein praktisch symmetrisches
Emissionsprofil, wie es auf dem Titelbild dargestellt ist!
an, fangen die beiden zweiten Integrale an, merklich beitzutragen,
und das photosphärische Profil wird langsam aufgefüllt, wobei das
Resultat aufgrund der Asymmetrie des ersten Anteils ein asymmetrisches Profil
ergibt. Bei sehr hohen Massenverlustraten dominiert schließlich der zweite
Term vollständig, und wir erhalten ein praktisch symmetrisches
Emissionsprofil, wie es auf dem Titelbild dargestellt ist!
In diesem Fall ist, unabhängig von jeglicher Theorie des
Strahlungstransportes, die H![]() -Emission einfach zu verstehen. Wir sehen im
wesentlichen Photonen, die in einem sehr großen Volumen emittiert werden,
u.zw. aufgrund der Elektronenkaskade von Niveau 3 auf Niveau 2. Da es sich
hierbei um zusätzliche Photonen (verglichen mit dem rein stellaren
Kontinuum) handelt, mußdas Profil in Emission erscheinen. Um die
Form des Profiles allerdings zu verstehen, sollte man sich auf jeden Fall den
Einflußdes Dopplereffekts vor Augen führen.
-Emission einfach zu verstehen. Wir sehen im
wesentlichen Photonen, die in einem sehr großen Volumen emittiert werden,
u.zw. aufgrund der Elektronenkaskade von Niveau 3 auf Niveau 2. Da es sich
hierbei um zusätzliche Photonen (verglichen mit dem rein stellaren
Kontinuum) handelt, mußdas Profil in Emission erscheinen. Um die
Form des Profiles allerdings zu verstehen, sollte man sich auf jeden Fall den
Einflußdes Dopplereffekts vor Augen führen.
Roberto Saglia