Next: Der Röntgensatellit ROSAT Up: Thermische Evolution von Neutronensternen Previous: Das FP-Modell (Friedman &
![]()
![]()
![]()
Next: Der Röntgensatellit ROSAT
Up: Thermische Evolution von Neutronensternen
Previous: Das FP-Modell (Friedman &
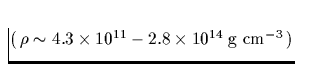 und den neutronenreichen
Gitterbausteinen der in dieser Region mit den superfluiden Neutronen
koexistierenden kristallinen Materie.
und den neutronenreichen
Gitterbausteinen der in dieser Region mit den superfluiden Neutronen
koexistierenden kristallinen Materie.
Der theoretisch vorhergesagte Einfluß der Reibungsheizung auf die
thermische Evolution von Neutronensternen ist insgesamt sehr groß
und führt besonders bei Pulsaren mit einem Alter von 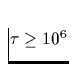 Jahren zu einer deutlich höheren thermischen Emission und
Röntgenleuchtkraft als im Fall einer fehlenden Reibungsheizung.
Das belegen sowohl die von Shibazaki & Lamb (1989) für einen
Neutronenstern im isothermen Gleichgewicht durchgeführten
Modellrechnungen als auch die von Umeda et al (1993) veröffentlichten
Ergebnisse, die dieser Einschränkung bereits nicht mehr unterliegen.
Für die durch Dissipation freigesetzte Heizleistung spezifizieren
die gegenwärtigen Theorien Werte im Bereich
Jahren zu einer deutlich höheren thermischen Emission und
Röntgenleuchtkraft als im Fall einer fehlenden Reibungsheizung.
Das belegen sowohl die von Shibazaki & Lamb (1989) für einen
Neutronenstern im isothermen Gleichgewicht durchgeführten
Modellrechnungen als auch die von Umeda et al (1993) veröffentlichten
Ergebnisse, die dieser Einschränkung bereits nicht mehr unterliegen.
Für die durch Dissipation freigesetzte Heizleistung spezifizieren
die gegenwärtigen Theorien Werte im Bereich 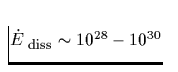 erg/s, die insbesondere
bei alten Neutronensternen zu einer über zehn- bis hundertmillionen
Jahre anhaltenden Erwärmung der Neutronensternoberfläche von
etwa 105
erg/s, die insbesondere
bei alten Neutronensternen zu einer über zehn- bis hundertmillionen
Jahre anhaltenden Erwärmung der Neutronensternoberfläche von
etwa 105 ![]() führen können.
führen können.
| 3c
TABELLE 2.1 |
||
| 3c | ||
| 3c | ||
| Reaktionsprozeß | Darstellung | Emissivität |
| (erg/s/cm3) | ||
| Direkter URCA-Prozeß | 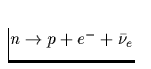
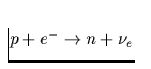 |
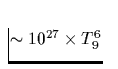 |
| |
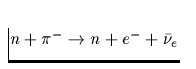
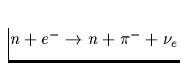 |
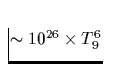 |
| Quark-URCA-Prozeß | 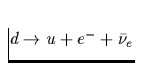
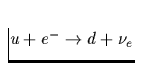 |
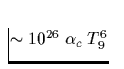 |
| K-Kondensat | 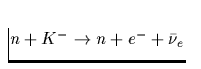
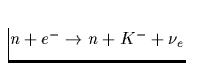 |
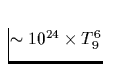 |
| Modifizierter URCA-Prozeß | 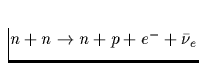
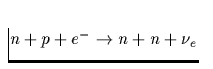 |
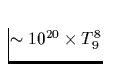 |
| Direkt gekoppelte
Elektron-Neutrino-Prozesse |
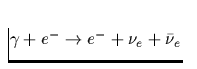 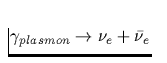 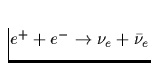 |
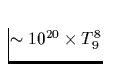 |
| Neutron-Neutron und Neutron-
Proton-Bremsstrahlung |
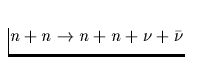
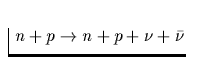 |
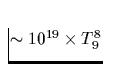 |
| Elektron-Ion-Neutrino-
Bremsstrahlung |
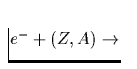
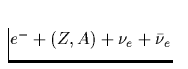 |
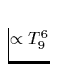 |
| 3c |
Tab. 2.1 Die vorstehende Tabelle zeigt
die wichtigsten zur Kühlung eines Neutronensterns beitragenden
Neutrino-Reaktionsprozesse, ihre Emissivität sowie deren
Temperaturabhängigkeit, zu der jedes n,p,e- einen Faktor T und jedes
Neutrino zusätzlich einen Faktor T3 beiträgt. Da die freie Weglänge
der Neutrinos wesentlich größer ist als der Radius des Neutronensterns,
verlassen die Neutrinos den Neutronenstern ohne Energieverlust und weitere
Wechselwirkungen. Entsprechend Fermi's Goldener Regel unterscheidet man
zwischen einer schnellen und einer langsamen Neutrinoemission, je nachdem,
ob an der Reaktion zwei oder vier Baryonen beteiligt sind. Bemerkenswert
ist die Vielzahl der möglichen Neutrinoprozesse. Die ersten vier der in der
Tabelle gezeigten Reaktionen führen auf eine um Größenordnungen höhere
Neutrinoemissivität, und bewirken damit eine wesentlich schnellere Abkühlung
des Neutronensterne, als die letzen vier Reaktionen, welche man mit dem Begriff
Standard-Kühlung zusammenfaßt.
Roberto Saglia